SHAZAM Moving Averages and Exponential Smoothing

Moving Averages and Exponential Smoothing

The SMOOTH command provides features for smoothing data by methods of moving averages and exponential smoothing.

Consider a time series with observed values X1, X2, ..., XN. A centered 5-point moving average is obtained as:

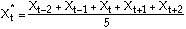      moving average formula       for   t = 3, ..., N-2

The number of periods used in calculating the moving average is specified with the NMA= option on the SMOOTH command.

The simple exponential smoothing method is based on a weighted average of current and past observations, with most weight to the current observation and declining weights to past observations. This gives the formula for the smoothed series as:

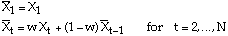
      exponential smoothing formula

where w is a smoothing constant with a value in the range [0,1]. The value for w is specified with the WEIGHT= option on the SMOOTH command.

Example

This example analyzes annual sales data (in thousands of dollars) of Lydia E. Pinkham from 1931 to 1960. The data set is listed in Newbold [1995, p. 691]. The SHAZAM commands (filename: MASMOOTH.SHA) below use the SMOOTH command to calculate a centered 5-point moving average and a series smoothed by exponential smoothing. 

SAMPLE 1 30
READ SALES / BYVAR
 1806  1644  1814  1770  1518  1103  1266  1473  1423  1767
 2161  2336  2602  2518  2637  2177  1920  1910  1984  1787
 1689  1866  1896  1684  1633  1657  1569  1390  1387  1289
GENR YEAR=TIME(1930)
* Set the smoothing constant for exponential smoothing.
GEN1 A=0.4
GEN1 W=1-A
SMOOTH SALES / NMA=5 WEIGHT=W MAVE=MA5 

* Graph the original data
GRAPH SALES YEAR / LINEONLY
* Graph the smoothed series
SAMPLE 3 28
GRAPH MA5 YEAR / LINEONLY
STOP

The SHAZAM output can be viewed. The results for a centered 5-point moving average are listed on the SHAZAM output in the column MOVING-AVE (see Newbold [1995, Table 17.12, p. 698]). The results from exponential smoothing are listed in the column EXP-MOV-AVE (see Newbold [1995, Table 17.16, p. 710]).

In the above SHAZAM commands, the MAVE= option on the SMOOTH command is used to save the moving average in the variable MA5. The GRAPH command is then used to graph the results.

A graph of the sales data is shown below (see Newbold [1995, Figure 17.6, p. 695]).

plot

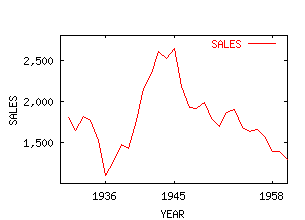
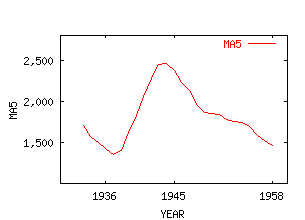
The next graph shows the series smoothed by moving averages (see Newbold [1995, Figure 17.7, p. 698]).

plot

Forecasting with Exponential Smoothing

Exponential smoothing methods use recursive updating formula to generate forecasts. A comparison of these methods with ARIMA models is given in Mills [1990, pp. 153-163]. The recursive formula required by exponential smoothing methods can be programmed in SHAZAM. This is shown with examples from Newbold [1995, Chapter 17].

References

Terence C. Mills, Time Series Techniques for Economists, 1990, Cambridge University Press.

Paul Newbold, Statistics for Business & Economics, Fourth Edition, 1995, Prentice-Hall.

Home [SHAZAM Guide home]

SHAZAM output - Moving Averages and Simple Exponential Smoothing 

 |_SAMPLE 1 30
 |_READ SALES / BYVAR
    1 VARIABLES AND       30 OBSERVATIONS STARTING AT OBS       1

 |_GENR YEAR=TIME(1930)
 |_* Set the smoothing constant for exponential smoothing.
 |_GEN1 A=0.4
 |_GEN1 W=1-A

 |_SMOOTH SALES / NMA=5 WEIGHT=W MAVE=MA5

 CENTRAL MOVING AVERAGES - PERIODS=  5 NSPAN=  1 WEIGHT= 0.600
 OBSERVATION  SALES    MOVING-AVE   SEAS&IRREG  SA(SALES   ) EXP-MOV-AVE
          1   1806.0      -------      -------       1806.0       1806.0
          2   1644.0      -------      -------       1644.0       1708.8
          3   1814.0       1710.4       1.0606       1814.0       1771.9
          4   1770.0       1569.8       1.1275       1770.0       1770.8
          5   1518.0       1494.2       1.0159       1518.0       1619.1
          6   1103.0       1426.0      0.77349       1103.0       1309.4
          7   1266.0       1356.6      0.93322       1266.0       1283.4
          8   1473.0       1406.4       1.0474       1473.0       1397.2
          9   1423.0       1618.0      0.87948       1423.0       1412.7
         10   1767.0       1832.0      0.96452       1767.0       1625.3
         11   2161.0       2057.8       1.0502       2161.0       1946.7
         12   2336.0       2276.8       1.0260       2336.0       2180.3
         13   2602.0       2450.8       1.0617       2602.0       2433.3
         14   2518.0       2454.0       1.0261       2518.0       2484.1
         15   2637.0       2370.8       1.1123       2637.0       2575.9
         16   2177.0       2232.4      0.97518       2177.0       2336.5
         17   1920.0       2125.6      0.90327       1920.0       2086.6
         18   1910.0       1955.6      0.97668       1910.0       1980.6
         19   1984.0       1858.0       1.0678       1984.0       1982.7
         20   1787.0       1847.2      0.96741       1787.0       1865.3
         21   1689.0       1844.4      0.91574       1689.0       1759.5
         22   1866.0       1784.4       1.0457       1866.0       1823.4
         23   1896.0       1753.6       1.0812       1896.0       1867.0
         24   1684.0       1747.2      0.96383       1684.0       1757.2
         25   1633.0       1687.8      0.96753       1633.0       1682.7
         26   1657.0       1586.6       1.0444       1657.0       1667.3
         27   1569.0       1527.2       1.0274       1569.0       1608.3
         28   1390.0       1458.4      0.95310       1390.0       1477.3
         29   1387.0      -------      -------       1387.0       1423.1
         30   1289.0      -------      -------       1289.0       1342.7
          1 SEASONAL FACTORS
          1   1.0000
 
 |_* Graph the original data
 |_GRAPH SALES YEAR / LINEONLY

        30 OBSERVATIONS
  SHAZAM WILL NOW MAKE A PLOT FOR YOU
  NO SYMBOLS WILL BE PLOTTED, LINE ONLY

 |_* Graph the smoothed series
 |_SAMPLE 3 28
 |_GRAPH MA5 YEAR / LINEONLY

        26 OBSERVATIONS
  SHAZAM WILL NOW MAKE A PLOT FOR YOU
  NO SYMBOLS WILL BE PLOTTED, LINE ONLY
 |_STOP
Home [SHAZAM Guide home]