Option Pricing The CALL and PUT commands provide features for pricing call and put options. Some sources on the internet are: Chicago Board Options Exchange - glossary Chicago Mercantile Exchange Example This example is from Clewlow and Strickland [1998, p. 21]. The problem is to price an at-the-money (ATM) European call option with a current asset price of $100. For an ATM option the exercise price is the same as the current price. Consider a one-year maturity (TIME=1) and assume the asset volatility is 20% (SIGMA=0.2) and the continuously compounded interest rate is 6 per cent per annum (RISKFREE=6). The SHAZAM commands below implement calculations for the general additive binomial tree method with three time steps in the binomial tree (NUMTIME=3) and for the Black-Scholes method. SAMPLE 1 1 GENR S=100 GENR K=100 * Binomial option pricing GENR N=3 CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 NUMTIME=N * Black-Scholes option pricing CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 BLACK STOP A comparison of the results is shown in the SHAZAM output below. The binomial method provides a call option price of $11.59 and the Black-Scholes formula gives a call option price of $10.99. |_SAMPLE 1 1 |_GENR S=100 |_GENR K=100 |_GENR N=3 |_CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 NUMTIME=N GENERAL ADDITIVE BINOMIAL TREE OF EUROPEAN CALL OBS TIME STOCK STRIKE RATE N UP DOWN DIV SIG CALL IMPVOL PCALL 1 1.00 100.00 100.00 6.00 3 0.00 0.20 0.000 11.592 |_CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 BLACK BLACK-SCHOLES MODEL-EUROPEAN CALL OBS TIME STOCK STRIKE RATE N UP DOWN DIV SIG CALL IMPVOL PCALL 1 1.00 100.00 100.00 6.00 0 0.00 0.20 0.000 10.990 Model Comparison Consider the above problem of pricing a one-year maturity, at-the-money (ATM) European call option with a current asset price of $100. Assume the continuously compounded interest rate is 6 per cent per annum. The figure below shows a comparison of call values from the general additive binomial tree valuation (with three time steps in the binomial tree) and the Black-Scholes valuation for different standard deviations. 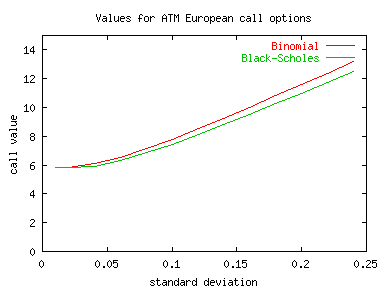Now consider the valuation when the asset volatility is assumed to be 20% (a standard deviation of 0.20). The figure below shows the convergence behavior for the price of the European call option for the general additive binomial tree valuation compared to the Black-Scholes valuation. 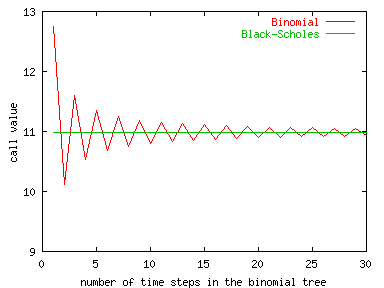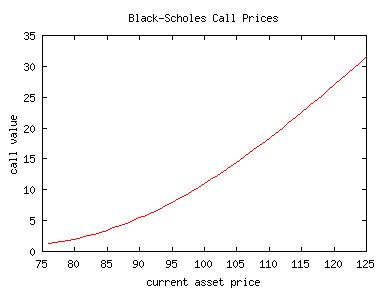The next figure shows Black-Scholes prices for a one-year maturity, European call option with a strike price of $100 with the assumptions that the continuously compounded interest rate is 6 per cent per annum and the standard deviation of the asset price is 0.20. The figure shows that the call option price goes to zero as the asset price falls way below the strike price. The SHAZAM commands below were used to generate the figures. SAMPLE 1 1 GENR S=100 GENR K=100 SAMPLE 1 13 READ STD / BYVAR 0.01 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20 0.22 0.24 GENR A=0 GENR B=0 SAMPLE 1 1 SET NOOUTPUT NODOECHO DO #=1,13 GEN1 SIG=STD:# * Binomial option pricing CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=SIG NUMTIME=3 PREDICTP=AP GEN1 A:#=AP * Black-Scholes option pricing CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=SIG BLACK PREDICTP=BP GEN1 B:#=BP ENDO SAMPLE 1 13 GRAPH A B STD / LINEONLY STOP SAMPLE 1 1 GENR S=100 GENR K=100 SAMPLE 1 1 GEN1 NBT=30 DIM A NBT B NBT * Black-Scholes option pricing CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 BLACK PREDICTP=BS * Binomial option pricing SET NOOUTPUT NODOECHO DO #=1,NBT GEN1 N=# CALL S / STRIKE=K TIME=1 RISKFREE=6 SIGMA=0.2 NUMTIME=N PREDICTP=AP GEN1 A:#=AP ENDO SAMPLE 1 NBT GENR B=BS GENR NTIME=TIME(0) GRAPH A B NTIME / LINEONLY STOP SAMPLE 1 1 GEN1 NBT=50 SAMPLE 1 NBT GENR SPRICE=75+TIME(0) SET NOOUTPUT * Black-Scholes option pricing CALL SPRICE / STRIKE=100 TIME=1 RISKFREE=6 SIGMA=0.2 BLACK PREDICTP=C GRAPH C SPRICE / LINEONLY STOP [SHAZAM Guide home]