Unbiased Estimators and their Sampling Distribution
Consider the random variables X1, X2, ..., Xn as a random sample from a population with mean µ. The average value of these observations is the sample mean. The sample mean is a random variable that is an estimator of the population mean. The expected value of the sample mean is equal to the population mean µ. Therefore, the sample mean is an unbiased estimator of the population mean.
How does this work in practice ? Suppose that a data set is collected with n numerical observations x1, x2, ..., xn. A numerical estimate of the population mean can be calculated. Since only a sample of observations is available, the estimate of the mean can be either less than or greater than the true population mean. If the sampling experiment was repeated a second time then a different set of numerical observations would be obtained. Therefore, the estimate of the population mean would be different from the estimate calculated from the first sample. However, the average of the estimates calculated over many repetitions of the sampling experiment will equal the true population mean.
This can be illustrated with a computer simulation. Suppose that a sample of 8 observations is drawn from a population that has a uniform distribution on the interval [0,4]. That is, the population mean is 2.
A computer program is used to generate 1000 different samples of 8 observations. An estimate of the mean is calculated for each sample. The results for the first 50 trials are shown below.
---------------- Sample Observations --------------- Sample
Trial x1 x2 x3 x4 x5 x6 x7 x8 Mean
1 0.884 3.816 0.663 0.412 0.523 3.934 3.425 0.553 1.776
2 2.033 0.538 2.475 3.411 3.647 2.608 3.875 3.183 2.721
3 1.083 0.111 0.804 3.485 1.739 3.021 2.601 2.469 1.914
4 2.579 1.017 0.362 3.455 1.312 0.280 0.906 0.295 1.276
5 2.733 3.816 3.824 3.573 2.394 2.991 2.409 3.264 3.126
6 0.376 0.346 2.247 0.884 2.836 1.334 2.225 2.217 1.558
7 1.753 2.217 3.492 3.006 1.260 2.859 1.230 2.888 2.338
8 3.522 2.792 3.360 1.069 3.301 2.549 2.380 2.586 2.695
9 1.260 2.152 3.699 0.789 1.385 0.671 2.093 3.050 1.887
10 0.214 3.345 2.085 0.273 1.415 0.907 2.292 3.080 1.701
11 1.739 2.483 2.189 2.321 1.047 3.794 0.627 1.010 1.901
12 2.785 1.282 0.619 2.932 2.336 0.789 0.405 1.341 1.561
13 0.030 0.744 2.034 2.262 1.024 1.496 2.262 1.290 1.393
14 0.111 2.446 2.903 1.650 2.615 2.431 0.361 1.540 1.757
15 3.521 1.856 1.024 0.832 1.724 1.142 2.578 0.973 1.706
16 2.917 2.954 3.839 3.183 3.699 3.801 2.748 2.579 3.215
17 1.106 2.225 2.984 2.520 1.828 3.596 3.316 3.854 2.678
18 3.853 3.588 0.848 0.664 3.176 1.761 1.717 2.314 2.240
19 3.603 0.804 3.714 2.218 2.734 1.423 1.431 1.188 2.139
20 3.317 3.943 2.167 1.791 2.801 2.535 1.666 1.828 2.506
21 2.263 3.508 2.079 2.602 2.072 0.532 0.805 0.068 1.741
22 3.273 1.122 0.989 0.841 3.972 3.162 3.449 2.536 2.418
23 1.482 2.469 0.628 1.541 0.142 1.401 3.346 1.512 1.565
24 2.050 3.346 1.328 2.691 1.586 3.236 0.503 0.260 1.875
25 0.260 1.233 1.380 3.538 3.288 2.949 0.260 1.807 1.839
26 3.604 1.483 2.743 2.426 1.630 0.186 1.336 3.163 2.071
27 0.430 1.866 3.546 0.651 2.684 2.625 1.078 0.304 1.648
28 2.500 1.004 0.356 0.231 0.415 3.899 1.534 3.501 1.680
29 1.564 2.890 1.741 0.886 3.641 0.363 2.433 0.989 1.814
30 0.268 1.873 1.343 0.120 3.184 0.238 0.216 2.897 1.267
31 3.987 2.455 1.962 1.431 1.048 0.827 0.009 0.805 1.566
32 0.378 2.757 2.883 2.956 2.905 1.174 2.013 2.595 2.208
33 1.292 2.080 0.290 2.934 0.695 1.373 0.621 1.874 1.395
34 0.327 2.979 3.200 3.885 3.656 3.929 2.743 3.848 3.071
35 3.752 0.040 0.290 2.051 2.987 1.543 2.950 0.084 1.712
36 1.506 1.749 2.198 3.200 0.998 2.294 2.147 3.856 2.243
37 0.799 1.108 0.990 0.799 2.979 1.336 2.721 1.639 1.546
38 3.952 2.773 3.819 1.336 0.011 0.578 0.025 3.171 1.958
39 0.187 3.996 0.173 2.876 2.309 3.885 0.813 3.686 2.241
40 2.912 1.690 1.602 2.927 0.939 3.244 3.871 3.650 2.604
41 0.703 1.845 3.466 0.504 3.370 3.370 1.374 1.028 1.957
42 3.105 0.446 1.705 1.779 3.599 2.339 0.976 0.342 1.786
43 1.654 2.494 2.759 2.663 1.787 3.223 1.035 1.448 2.133
44 3.511 2.258 3.356 2.604 0.564 0.549 1.175 3.533 2.194
45 2.339 3.503 1.919 3.820 0.004 0.203 2.803 2.899 2.186
46 1.904 0.122 0.262 1.190 0.387 1.713 2.560 2.052 1.274
47 2.855 2.111 2.796 1.403 2.862 1.728 2.435 1.971 2.270
48 3.599 3.937 3.525 2.177 0.269 1.175 2.994 1.926 2.450
49 3.356 0.387 2.472 0.144 1.757 0.277 3.901 1.617 1.739
50 2.634 3.864 2.162 0.844 3.356 0.070 3.805 2.354 2.386
|
By viewing the final column that lists the estimates of the mean it can be seen that some estimates are less than the population mean of 2 and some estimates are greater than 2. A total of 1000 estimates was calculated and the average was obtained as:
2.00780
The closeness of the average to 2 (the true population mean) reflects that the estimates are generated from an unbiased estimation procedure.
The sampling distribution of an estimator is the distribution of the estimator in all possible samples of the same size drawn from the population. For the sample mean, the central limit theorem gives the result that the sampling distribution of the sample mean will tend to the normal distribution. To see this result, the 1000 estimates of the mean were sorted into a number of groups. The numbers of observations in each group are displayed in the histogram below.
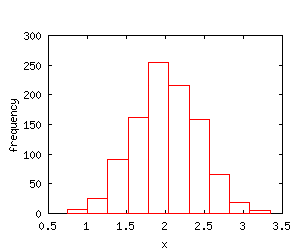
The above histogram is centered at 2 (the value of the population mean) and the shape conforms to the shape of a normal distribution.
SHAZAM command file
The SHAZAM commands for the above demonstration are as follows.
SAMPLE 1 8 GEN1 NREP=1000 * Repeated sampling of observations from a uniform distribution * with sample size 8 DIM SAMPMEAN NREP SET NODOECHO NOOUTPUT RANFIX DO #=1,NREP * Generate the sample GENR X=UNI(4) * Calculate the sample mean STAT X / MEAN=MEAN * Save the results MATRIX I=$DO MATRIX RESULTS=(I|X'|MEAN) FORMAT(1X,F5.0,8F7.3,3X,F7.3) IF (I.LE.50) PRINT RESULTS / FORMAT NONAMES GEN1 SAMPMEAN:#=MEAN ENDO * Get the average from all the replications SET OUTPUT SAMPLE 1 NREP STAT SAMPMEAN / MEAN=MEAN PRINT MEAN * Display the sampling distribution with a histogram GRAPH SAMPMEAN / HISTO GROUPS=10 RANGE STOP |
 [SHAZAM Guide home]
[SHAZAM Guide home]