Prediction with a Log-Transformed Dependent Variable
This discussion continues with the analysis of voting patterns in the state of Florida for the United States 2000 presidential election. A linear regression equation that relates Buchanan's votes to Bush's votes in the counties of Florida may feature heteroskedastic errors arising from an error variance that is positively related to population size.
A possible test for heteroskedasticity is to estimate a separate regression equation for the counties that rank in the top 25% for the total number of votes and for the counties with total number of votes less than the value for the upper quartile. A test for equal error variance in the two groups can then be implemented. This test procedure is known as the Goldfeld-Quandt test. Note that the test requires the choice of a breakpoint for splitting the two groups of observations.
The SHAZAM commands below use the SORT
command to order the county observations (excluding Palm Beach county)
by the total number of votes. In the ordered data set, the first
observation is the county with the smallest number of total votes.
The final observation, Palm Beach county, is the target county
for the prediction exercise.
The DIAGNOS command that follows the
OLS estimation command is used to compute
a Goldfeld-Quandt test for heteroskedasticity.
The number of observations in the first group is specified with the
CHOWONE= option.
SAMPLE 1 67 READ (PRES2000.txt) GORE BUSH BUCHANAN NADER OTHER / SKIPLINE=1 * Exclude Palm Beach County SAMPLE 1 66 GENR TOTAL=GORE+BUSH+BUCHANAN+NADER+OTHER SORT TOTAL GORE BUSH BUCHANAN NADER OTHER GEN1 N75=INT(66*.75) * Estimate a linear relationship between Buchanan/Bush votes OLS BUCHANAN BUSH * Test for heteroskedasticity DIAGNOS / HET CHOWONE=N75 * Transform the data to logarithms and estimate a log-log model. SAMPLE 1 67 DIM YHAT 67 SE 67 GENR LBUCHNN=LOG(BUCHANAN) GENR LBUSH=LOG(BUSH) SAMPLE 1 66 OLS LBUCHNN LBUSH / LOGLOG * Test for heteroskedasticity DIAGNOS / HET CHOWONE=N75 * Log prediction for Buchanan in Palm Beach. FC / LIST BEG=67 END=67 PREDICT=YHAT FCSE=SE * Calculate a 99% prediction interval * Obtain the critical value. GEN1 DF=$N-$K SAMPLE 1 1 GEN1 ALPHA=0.01/2 DISTRIB ALPHA / TYPE=T DF=DF INVERSE CRITICAL=TC SAMPLE 67 67 * Estimate a confidence interval for the log prediction GENR YUP=YHAT+TC*SE GENR YLOW=YHAT-TC*SE * Estimate a confidence interval for the anti-log prediction GENR YUP=EXP(YUP) GENR YLOW=EXP(YLOW) * Estimate the anti-log point prediction GENR YHAT=EXP(YHAT+SE*SE/2) * Print the results. PRINT YLOW YHAT YUP * The prediction interval is not symmetric about the point prediction. STOP |
The SHAZAM output can be viewed.
For the simple linear regression equation of the Buchanan-Bush
vote relationship the Goldfeld-Quandt test statistic is calculated as
the ratio of the estimated error variance for the "small-medium"
counties to the estimated error variance for the "large" counties.
The SHAZAM output reports a test statistic value
0.0674. For a test of the null hypothesis
of equal error variance against the alternative hypothesis of larger
error variance for the "large" counties the p-value is less than
0.0005. This gives strong evidence for the presence
of heteroskedastic errors.
The above SHAZAM commands transform the vote data to logarithms
and estimate a linear regression equation with the log-transformed
data (excluding Palm Beach county).
For this model, the Goldfeld-Quandt test statistic is reported
as 1.432. Since the test value is greater than
one, the estimated error variance for the first group exceeds
the estimated error variance for the second group.
A rejection rule for the null hypothesis of equal error variance is obtained
by comparing the test statistic with values from an
F distribution with
P(F(47,15) > 1.432) = 0.227
The p-value exceeds the usual significance levels and therefore there is evidence that the log-linear model has homoskedastic errors.
The results from the log-linear regression can be used to predict the log of the Buchanan vote for Palm Beach county. For a meaningful interpretation of the results, the log prediction must then be converted to a prediction for the number of votes. A useful discussion about the calculation of point predictions and prediction intervals when the dependent variable is log-transformed is Nelson [1973, pp. 161-165].
Denote the observations on the dependent variable as:
zt = log(yt)
Based on a linear regression model, suppose the point prediction for an observation z0 is:
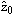
and the estimated standard error of the prediction is:
se(e0)
A prediction interval estimate for z0 is:
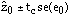
where tc is an appropriate t-distribution critical value.
Assuming the errors for the log-linear regression equation are normally distributed, the antilog point prediction for
y0 = exp(z0) is:
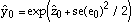
and a prediction interval estimate for y0 is:
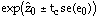
Note that the interval estimate for the anti-log prediction is not symmetric about the point prediction estimate.
The above results were applied to obtain a prediction of
the number of votes for Buchanan in Palm Beach county based on
a log-linear regression that relates Buchanan's vote to Bush's vote in the
other 66 Florida counties.
The calculations show that the predicted number of
votes for Buchanan in Palm Beach county is 656
and the 99% prediction interval estimate is:
[190 , 1875]
The interval estimate obtained from the log-linear model is wider
than the interval estimate calculated from the simple linear regression
equation.
However, the results still show that the Buchanan vote count of
3407 in Palm Beach county may be labelled as an outlier.
References
Charles R. Nelson, Applied Time Series Analysis for Managerial Forecasting, 1973, Holden-Day.
SHAZAM output
|_SAMPLE 1 67
|_READ (PRES2000.txt) GORE BUSH BUCHANAN NADER OTHER / SKIPLINE=1
UNIT 88 IS NOW ASSIGNED TO: PRES2000.txt
5 VARIABLES AND 67 OBSERVATIONS STARTING AT OBS 1
|_* Exclude Palm Beach County
|_SAMPLE 1 66
|_GENR TOTAL=GORE+BUSH+BUCHANAN+NADER+OTHER
|_SORT TOTAL GORE BUSH BUCHANAN NADER OTHER
DATA HAS BEEN SORTED BY VARIABLE TOTAL
|_GEN1 N75=INT(66*.75)
|_* Estimate a linear relationship between Buchanan/Bush votes
|_OLS BUCHANAN BUSH
OLS ESTIMATION
66 OBSERVATIONS DEPENDENT VARIABLE= BUCHANAN
...NOTE..SAMPLE RANGE SET TO: 1, 66
R-SQUARE = 0.7511 R-SQUARE ADJUSTED = 0.7472
VARIANCE OF THE ESTIMATE-SIGMA**2 = 12880.
STANDARD ERROR OF THE ESTIMATE-SIGMA = 113.49
SUM OF SQUARED ERRORS-SSE= 0.82430E+06
MEAN OF DEPENDENT VARIABLE = 213.00
LOG OF THE LIKELIHOOD FUNCTION = -404.927
VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY
NAME COEFFICIENT ERROR 64 DF P-VALUE CORR. COEFFICIENT AT MEANS
BUSH 0.34962E-02 0.2516E-03 13.90 0.000 0.867 0.8666 0.6857
CONSTANT 66.940 17.48 3.829 0.000 0.432 0.0000 0.3143
|_* Test for heteroskedasticity
|_DIAGNOS / HET CHOWONE=N75
DEPENDENT VARIABLE = BUCHANAN 66 OBSERVATIONS
REGRESSION COEFFICIENTS
0.349623785167E-02 66.9403199359
HETEROSKEDASTICITY TESTS
CHI-SQUARE D.F. P-VALUE
TEST STATISTIC
E**2 ON YHAT: 31.055 1 0.00000
E**2 ON YHAT**2: 43.351 1 0.00000
E**2 ON LOG(YHAT**2): 17.817 1 0.00002
E**2 ON LAG(E**2) ARCH TEST: 0.899 1 0.34314
LOG(E**2) ON X (HARVEY) TEST: 19.757 1 0.00001
ABS(E) ON X (GLEJSER) TEST: 56.839 1 0.00000
E**2 ON X TEST:
KOENKER(R2): 31.055 1 0.00000
B-P-G (SSR) : 133.086 1 0.00000
E**2 ON X X**2 (WHITE) TEST:
KOENKER(R2): 46.740 2 0.00000
B-P-G (SSR) : 200.303 2 0.00000
SEQUENTIAL CHOW AND GOLDFELD-QUANDT TESTS
N1 N2 SSE1 SSE2 CHOW PVALUE G-Q DF1 DF2 PVALUE
49 17 0.10622E+06 0.50292E+06 10.950 0.000 0.6740E-01 47 15 0.000
CHOW TEST - F DISTRIBUTION WITH DF1= 2 AND DF2= 62
|_* Transform the data to logarithms and estimate a log-log model.
|_SAMPLE 1 67
|_DIM YHAT 67 SE 67
|_GENR LBUCHNN=LOG(BUCHANAN)
|_GENR LBUSH=LOG(BUSH)
|_SAMPLE 1 66
|_OLS LBUCHNN LBUSH / LOGLOG
OLS ESTIMATION
66 OBSERVATIONS DEPENDENT VARIABLE= LBUCHNN
...NOTE..SAMPLE RANGE SET TO: 1, 66
R-SQUARE = 0.8652 R-SQUARE ADJUSTED = 0.8631
VARIANCE OF THE ESTIMATE-SIGMA**2 = 0.17662
STANDARD ERROR OF THE ESTIMATE-SIGMA = 0.42026
SUM OF SQUARED ERRORS-SSE= 11.304
MEAN OF DEPENDENT VARIABLE = 4.7965
LOG OF THE LIKELIHOOD FUNCTION(IF DEPVAR LOG) = -351.987
VARIABLE ESTIMATED STANDARD T-RATIO PARTIAL STANDARDIZED ELASTICITY
NAME COEFFICIENT ERROR 64 DF P-VALUE CORR. COEFFICIENT AT MEANS
LBUSH 0.72960 0.3599E-01 20.27 0.000 0.930 0.9302 0.7296
CONSTANT -2.3166 0.3547 -6.531 0.000-0.632 0.0000 -2.3166
|_* Test for heteroskedasticity
|_DIAGNOS / HET CHOWONE=N75
REQUIRED MEMORY IS PAR= 13 CURRENT PAR= 2000
DEPENDENT VARIABLE = LBUCHNN 66 OBSERVATIONS
REGRESSION COEFFICIENTS
0.729595970989 -2.31656542773
HETEROSKEDASTICITY TESTS
CHI-SQUARE D.F. P-VALUE
TEST STATISTIC
E**2 ON YHAT: 2.495 1 0.11421
E**2 ON YHAT**2: 2.025 1 0.15470
E**2 ON LOG(YHAT**2): 3.071 1 0.07971
E**2 ON LAG(E**2) ARCH TEST: 0.747 1 0.38727
LOG(E**2) ON X (HARVEY) TEST: 0.000 1 0.98734
ABS(E) ON X (GLEJSER) TEST: 1.126 1 0.28873
E**2 ON X TEST:
KOENKER(R2): 2.495 1 0.11421
B-P-G (SSR) : 2.402 1 0.12117
E**2 ON X X**2 (WHITE) TEST:
KOENKER(R2): 4.872 2 0.08750
B-P-G (SSR) : 4.691 2 0.09580
SEQUENTIAL CHOW AND GOLDFELD-QUANDT TESTS
N1 N2 SSE1 SSE2 CHOW PVALUE G-Q DF1 DF2 PVALUE
49 17 8.8998 1.9840 1.1956 0.309 1.432 47 15 0.227
CHOW TEST - F DISTRIBUTION WITH DF1= 2 AND DF2= 62
|_* Log prediction for Buchanan in Palm Beach.
|_FC / LIST BEG=67 END=67 PREDICT=YHAT FCSE=SE
DEPENDENT VARIABLE = LBUCHNN 1 OBSERVATIONS
REGRESSION COEFFICIENTS
0.729595970989 -2.31656542773
OBS. OBSERVED PREDICTED CALCULATED STD. ERROR
NO. VALUE VALUE RESIDUAL
67 8.1336 6.3928 1.7408 0.431 I *
SUM OF ABSOLUTE ERRORS= 1.7408
R-SQUARE BETWEEN OBSERVED AND PREDICTED = 0.0000
R-SQUARE BETWEEN ANTILOGS OBSERVED AND PREDICTED = 0.0000
MEAN ERROR = 1.7408
SUM-SQUARED ERRORS = 3.0305
MEAN SQUARE ERROR = 3.0305
MEAN ABSOLUTE ERROR= 1.7408
ROOT MEAN SQUARE ERROR = 1.7408
MEAN SQUARED PERCENTAGE ERROR= 458.09
THEIL INEQUALITY COEFFICIENT U = 0.000
DECOMPOSITION
PROPORTION DUE TO BIAS = 1.0000
PROPORTION DUE TO VARIANCE = 0.0000
PROPORTION DUE TO COVARIANCE = 0.0000
DECOMPOSITION
PROPORTION DUE TO BIAS = 1.0000
PROPORTION DUE TO REGRESSION = 0.0000
PROPORTION DUE TO DISTURBANCE = 0.0000
|_* Calculate a 99% prediction interval
|_* Obtain the critical value.
|_GEN1 DF=$N-$K
..NOTE..CURRENT VALUE OF $N = 66.000
..NOTE..CURRENT VALUE OF $K = 2.0000
|_SAMPLE 1 1
|_GEN1 ALPHA=0.01/2
|_DISTRIB ALPHA / TYPE=T DF=DF INVERSE CRITICAL=TC
T DISTRIBUTION DF= 64.000
VARIANCE= 1.0323 H= 1.0000
PROBABILITY CRITICAL VALUE PDF
ALPHA
ROW 1 0.50000E-02 2.6553 0.13308E-01
|_SAMPLE 67 67
|_* Estimate a confidence interval for the log prediction
|_GENR YUP=YHAT+TC*SE
|_GENR YLOW=YHAT-TC*SE
|_* Estimate a confidence interval for the anti-log prediction
|_GENR YUP=EXP(YUP)
|_GENR YLOW=EXP(YLOW)
|_* Estimate the anti-log point prediction
|_GENR YHAT=EXP(YHAT+SE*SE/2)
|_* Print the results.
|_PRINT YLOW YHAT YUP
YLOW YHAT YUP
190.4035 655.5699 1875.011
|_* The prediction interval is not symmetric about the point prediction.
|_STOP
 [SHAZAM Guide home]
[SHAZAM Guide home]